Berechnungsmethoden
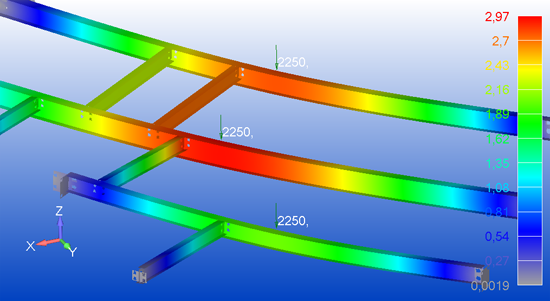
Lineare Statik
Viele Berechnungsaufgaben lassen sich mit linearer Statik lösen:
Die Verformung ist proportional zur einwirkenden Kraft, es besteht also ein linearer Zusammenhang.
Dabei sind die Verformungen klein im Vergleich zu den Bauteilabmessungen und es treten auch sonst keine nichtlinearen Effekte wie Kontakt oder Plastifizierung auf.

Nichtlineare Berechnung - Kontakt
Oft gibt es in der Technik belastungsabhängige Kontaktsituationen.
Ein einfaches Beispiel sind Bolzenverbindungen: je nach Kraftrichtung ändert sich der Kraftfluss in den beteiligten Bauteilen.
Ein weiteres Beispiel sind hochbelastete Schraubenverbindungen. Zwischen den verspannten Teilen bildet sich unter Belastung ein Spalt und der Zusammenhang zwischen Kraft und Verformung ist nicht mehr linear.
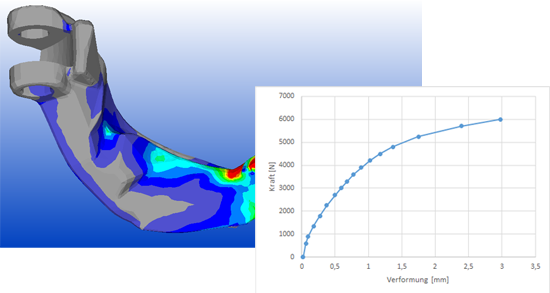
Nichtlineare Berechnung - plastische Verformung
Wird durch eine hohe Belastung die Streckgrenze eines Materials überschritten kommt es zu plastischen Verformungen. Das kann im Extremfall bis zur Bruchdehnung und damit dem endgültigen Versagen gehen.
Plastische Verformung bedeutet, dass ein Bauteil eine bleibende Verformung erfährt - nach Entlastung wird nicht mehr die ursprüngliche Form erreicht.
Relevant kann eine solche Betrachtung für Bauteile sein, die einerseits sehr leicht sein sollen und andererseits im Versagensfall eine bestimmte Energieaufnahme gewährleisten sollen (z.B. crash-beanspruchte Bauteile im Automobil-Bereich).
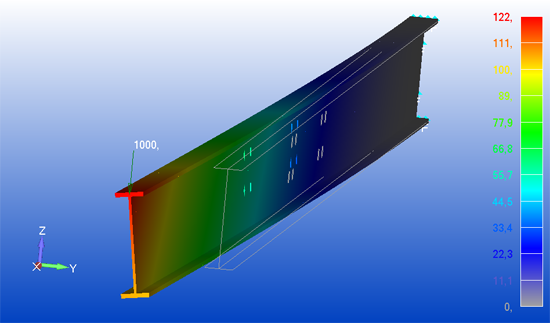
Nichtlineare Berechnung - große Verformungen
Von großen Verformungen spricht man in der Festigkeitslehre, wenn sich aufgrund der Verformung die Einwirkungen wesentlich ändern.
So können z.B. durch die Verformung zusätzliche Kräfte oder Momente entstehen, die bei der Berechnung berücksichtigt werden müssen. Man spricht dann von einem Gleichgewicht im verformten Zustand oder Theorie II. Ordnung.
Stabilitätsuntersuchungen
Bei einem Stabilitätsversagen verliert ein Bauteil seine Tragfähigkeit, bevor das Material versagt. Aufgrund von Druckspannung weicht die Geometrie aus – einfaches Beispiel: eine leere Cola-Dose. Das Material könnte noch mehr, aber das dünnwandige Blech knittert und faltet sich zusammen.
Weitere Stabilitätskriterien:
- Stabknicken
- Schalenbeulen
- Biegedrillknicken
Stabilitätsversagen tritt typischerweise bei schlanken oder dünnwandigen Strukturen unter Druckbelastung auf. Kuppel-Abdeckungen aus GFK sind ein gutes Beispiel: die Strukturen haben einen Durchmesser von bis zu 30m und die Wandstärken bewegen sich im Bereich von 5...25mm. Über eine Buckling-Analyse lassen sich die Sicherheiten gegen Stabilitätsversagen ermitteln.
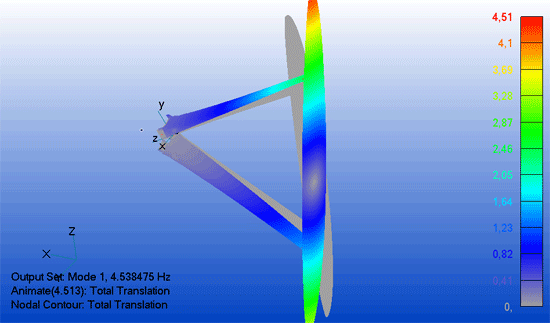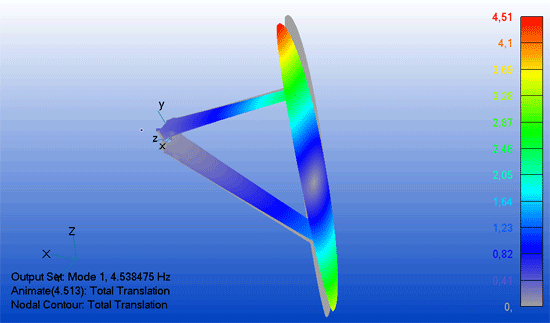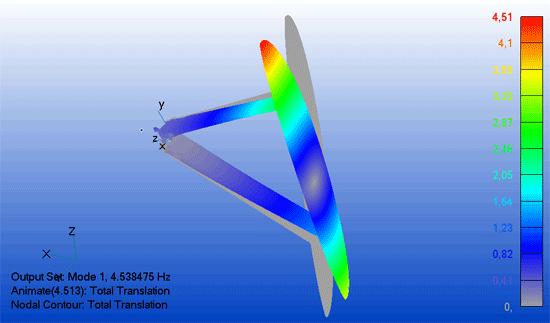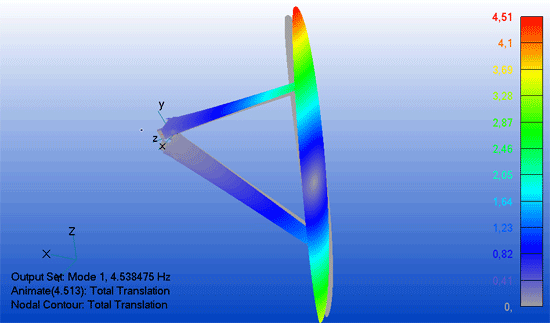
Eigenfrequenzen
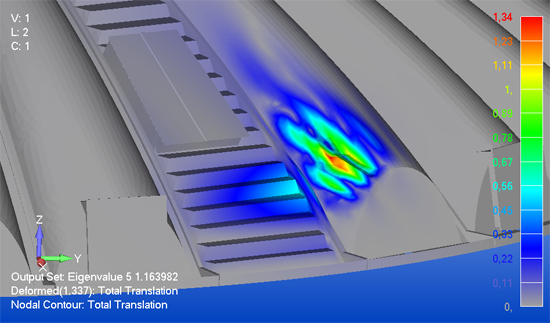
Wenn eine Struktur in ihrer Eigenfrequenz angeregt wird, kann sich eine Schwingung aufschaukeln - im schlimmsten Fall bis zum Versagen.
Die Erreger-Frequenz ist häufig bekannt, z.B. die Drehzahl des Antriebs. Was fehlt ist die Eigenfrequenz der Struktur, um eine Aussage über das Schwingungsverhalten zu treffen. Hier ist eine Eigenfrequenz-Analyse eine wertvolle Hilfe.
Zusatzprogramme und Hilfsmittel
Zahlreiche Hilfsprogramme und Makros ergänzen die Standard-FE-Software:
- Makros zur Berechnung von Schweißnaht-Vergleichsspannungen
- Makros für den Ermüdungsnachweis
- Schraubennachweis unter Verwendung des Application Programming Interface (API)
- Materialkennwerte für GFK/CFK nach Germanischem Lloyd abhängig von Lagenaufbau und Faservolumengehalt
- Materialkennwerte und Abminderungsfaktoren für GFK im Bauwesen nach DIN 18820
- Datenbank für unterschiedlichste Carbonfaser-Halbzeuge (Rovings, Bänder, Flechtschläuche, Gelege, Gewebe)
- Klassische Laminattheorie zur schnellen Vordimensionierung von Faserverbundstrukturen